베이즈 필터

분할 :

전확률 공식 :

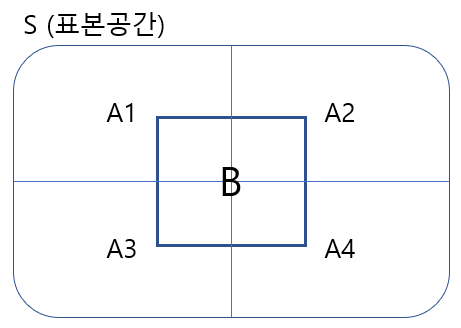
베이즈 정리 :

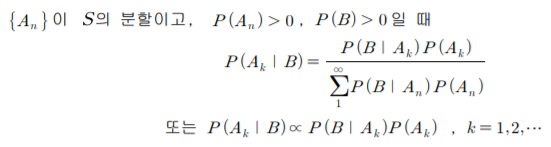
-추가설명 : 베이즈 정리에서 분모 항은 Ak와 무관하다. 이 때문에 분모 항을 정규화 항이라고 하며, 보통 η로 표시한다.

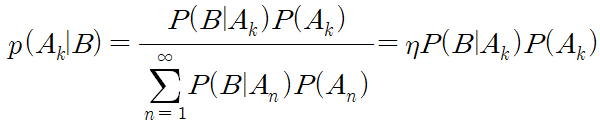
베이즈 필터 알고리즘 :

$x_{t}$=시간 t에서의 스테이트의 실제 상태

$u_{t}$=시간 t에서의 제어값

$z_{t}$=시간 t에서의 측정값

$bel(x_{t})$=$x_{t}$의 빌리프

3행 - 현재의 제엇값과 바로 이전의 빌리프를 이용해 현재 스테이트의 예측값을 계산 (예측 단계)

4행 - 3행에서 계산한 빌리프와 측정값이 나타날 확률을 이용해 현재 스테이트의 빌리프를 계산 (측정 업데이트 단계)

이 때, 빌리프는 가능한 모든 스테이트에 대한 빌리프를 모두 구한다(여기서 빌리프들은 η에 대한 함수로 나타남). 그 후, 모든 빌리프들의 합이 1이 되도록 η의 값을 구하면 각 스테이트의 빌리프를 구할 수 있다.

베이즈 필터 알고리즘은 재귀적인 특성을 가지는데, 이전의 모든 데이터를 남겨두는게 아닌 이전 스테이트에 대한 정보만 데이터로 남겨둬도 된다.

마르코프 가정 : 현재 스테이트$x_{t}$를 안다면 과거와 미래의 데이터가 독립적이라고 가정 -> 재귀적 특성을 가질 수 있게 하는 이론으로, 베이즈 필터 알고리즘의 토대가 되는 이론 중 하나이다.

베이즈 필터 알고리즘은 실용적인 알고리즘이 아니며, 이는 디지털 컴퓨터에서 구현할 수 없다는 점을 내포하고 있다. 이 때문에 확률적 알고리즘에서 다루기 쉬운 근사 기법을 사용한다 - 확률론적 로보틱스 인용

근사 기법으로는 칼만 필터, 히스토그램 필터, 파티클 필터 등이 있다.

stdy.c