- Euclidean clustering이란 데이터간 거리가 일정거리 이하이면 하나의 군집으로 묶는 알고리즘이다. 하지만 이를 아무런 전처리 없이 구현하면 모든 데이터간 거리를 계산해야 한다. 하지만 데이터를 필요에 맞게 구조화 시키면 모든 데이터간 거리를 계산하지 않아도 Euclidean clustering이 가능해진다. 데이터 구조화 방법 중 하나로 k-d tree가 있다.

- k-d tree란 이진 탐색 트리를 k차원으로 확장한 데이터 구조로, 삽입시 데이터는 각 차원을 번갈아 비교하여 트리구조에 저장된다.
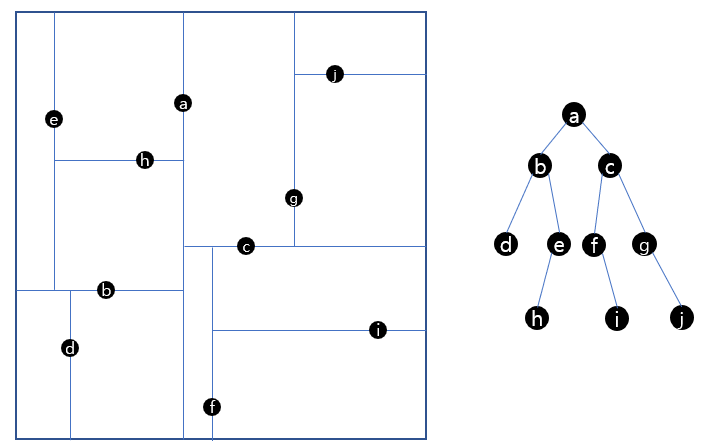
- k-d tree 구성 : 트리를 구성하는 방법에는 여러가지가 있는데, 균형 잡힌 k-d 트리를 만들기 위해 중앙값을 사용하는 방법이 있다. 2D의 경우 구성 단계는 다음과 같다.
1) 데이터들의 x축 기준 중앙값을 찾고 해당 데이터를 노드에 삽입한다.
2) 노드의 좌측에는 위에서 찾은 중앙값보다 x좌표가 작은 데이터들 중 y축 기준 중앙값의 데이터를 삽입하고, 노드의 우측에는 위에서 찾은 중앙값보다 x좌표가 큰 데이터들 중 y축 기준 중앙값의 데이터를 삽입한다.
3) 위 과정을 재귀적으로 수행한다.
*중앙값을 찾는 알고리즘에는 quick-select와 median-of-medians를 결합하여 O(n)의 시간에 중앙값을 찾는 알고리즘이 있다.
*C++ STL에서는 nth_element라는 함수를 제공하는데, 배열의 n번째 요소를 찾아주며, n번째 요소까지 정렬해준다.
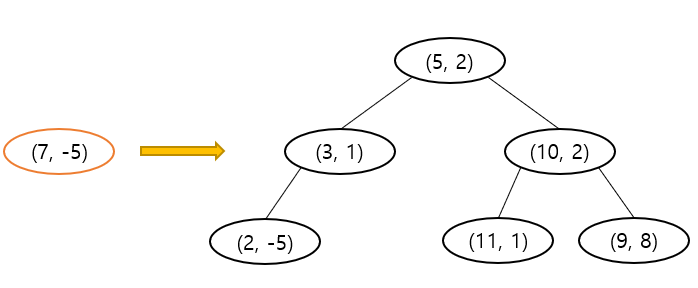
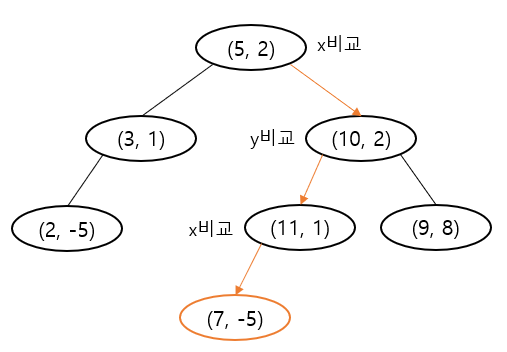
- k-d tree 삽입 : 2D의 경우 삽입 과정은 아래와 같다.
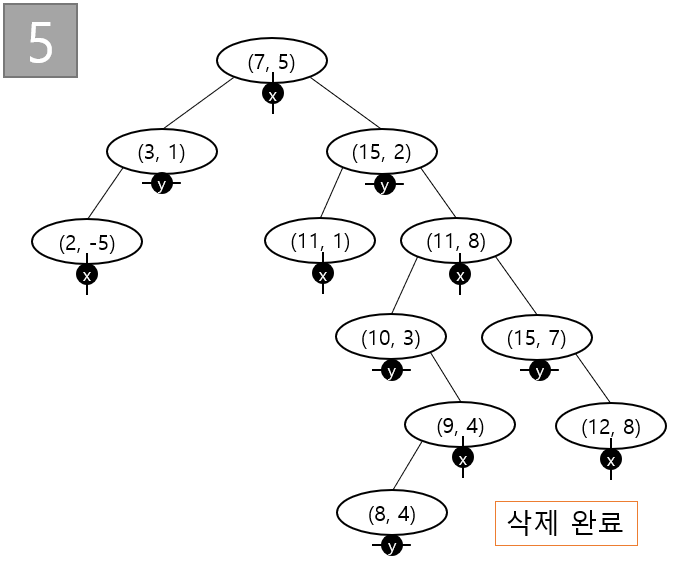
- k-d tree 삭제 : 삭제의 경우 과정은 다음과 같다.
1) 삭제하려는 노드의 오른쪽 자식이 있을 때,
삭제하려는 노드의 축에 해당하는 좌표의 최소값을 오른쪽 서브트리로부터 찾는다.
삭제하려는 노드의 데이터를 최소값을 갖는 노드의 데이터로 바꾼다.
오른쪽 서브트리의 최소값을 갖는 노드를 삭제한다.
2) 오른쪽 자식은 없는데 왼쪽 자식이 있을 때,
삭제하려는 노드의 축에 해당하는 좌표의 최소값을 왼쪽 서브트리로부터 찾는다.
삭제하려는 노드의 데이터를 최소값을 갖는 노드의 데이터로 바꾼다.
삭제하려는 노드의 왼쪽자식을 오른쪽자식으로 바꾼다.
오른쪽 서브트리의 최소값을 갖는 노드를 삭제한다.
3) 자식이 없을 때,
삭제하려는 노드를 삭제한다.
위 과정은 재귀적으로 수행된다.
*최소값 노드를 찾을 때는 k-d tree의 특성을 이용한다.
다음은 2D 삭제 예시이다.




- 구형 범위 탐색 : 2D의 경우 예시는 다음과 같다.






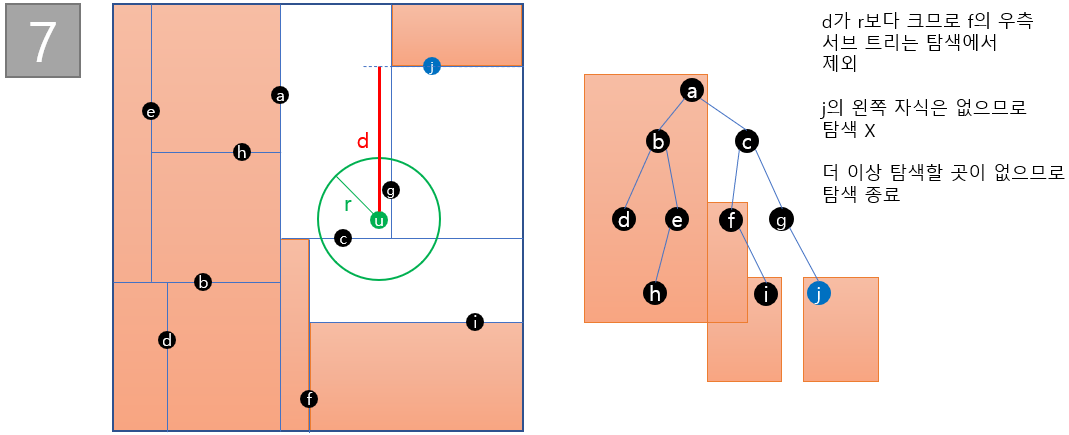
-----> 탐색 예시를 보면 탐색시 제외되는 부분이 많기 때문에 탐색 성능이 좋다. 단, 균형잡히지 않은 트리의 경우 탐색성능이 저하될 수 있다.
-----> Euclidean clustering에 k-d tree 구조를 사용하면 일반적으로 더 좋은 성능을 낸다.